Understanding Alternate Interior Angles: A Fascinating Aspect of Geometry

Geometry is a branch of mathematics that deals with shapes, sizes, and the properties of space. Among its many intriguing concepts, alternate interior angles stand out as an essential principle, forming the foundation for understanding parallel lines and transversals. Although the term may initially seem complex to some students, with a clear explanation and practical examples, alternate interior angles become not only understandable but also surprisingly fascinating.

What Are Alternate Interior Angles?

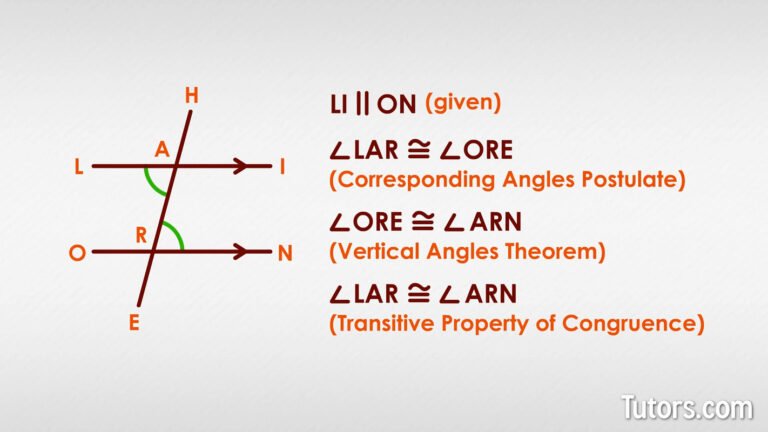
In simple terms, alternate interior angles are pairs of angles formed when a transversal intersects two lines. The word “interior” refers to the space between the two lines, and “alternate” indicates that the angles lie on opposite sides of the transversal.

For example, imagine two parallel lines crossed by a diagonal line. The angles formed on the inside of these parallel lines and on opposite sides of the transversal are alternate interior angles.

Mathematically, these angles have a special property: if the two lines are parallel, alternate interior angles are always equal. This property is incredibly useful in various geometrical proofs and real-world applications, making alternate interior angles one of the most powerful concepts in elementary geometry.

The Positive Importance of Alternate Interior Angles

Alternate interior angles may seem like a small concept in the grand scheme of mathematics, but their significance is immense. Understanding them helps in several ways:

1. Foundation for Parallel Lines: Recognizing alternate interior angles allows students and professionals to determine if two lines are parallel. If a pair of alternate interior angles are equal, it confirms the lines are parallel. This property is a cornerstone in geometry, used in proofs and problem-solving.
2. Simplifies Geometry Problems: Many geometry problems that involve triangles, quadrilaterals, or polygons become much easier to solve when alternate interior angles are understood. They allow mathematicians to find unknown angles without complex calculations.
3. Real-World Applications: From architecture to engineering, the principle of alternate interior angles is applied in designing structures, roads, bridges, and even in computer graphics. Ensuring precise angles and parallel alignments often relies on the understanding of this concept.

How to Identify Alternate Interior Angles

Identifying alternate interior angles requires careful observation. Here’s a simple step-by-step method:

1. Look for Two Lines: Start by identifying two straight lines in the diagram or problem.
2. Identify the Transversal: A transversal is a line that cuts across these two lines. Look for a line intersecting both of your lines at an angle.
3. Locate Interior Angles: Focus on the angles formed between the two lines. These are your interior angles.
4. Check Opposite Sides: From the interior angles, locate the ones on opposite sides of the transversal. These are your alternate interior angles.

For clarity, suppose lines $l_1$l1​ and $l_2$l2​ are parallel and a transversal $t$t cuts across them. The angles on the inside of the lines, one on the left of $t$t and the other on the right, are alternate interior angles. If $\angle A = \angle B$∠A=∠B, then the property holds true.

Visualizing Alternate Interior Angles

While diagrams are typically helpful, you can also visualize alternate interior angles mentally. Imagine a ladder leaning across two parallel rails. The steps of the ladder form angles with the rails. The angles on opposite sides of the ladder but between the rails represent alternate interior angles. Even without drawing, this mental image helps students and learners grasp the concept intuitively.

Examples of Alternate Interior Angles in Use

1. Mathematical Problem Solving:
   Consider two parallel lines intersected by a transversal. One interior angle measures 65°. By the property of alternate interior angles, the angle on the opposite side of the transversal inside the parallel lines also measures 65°. This simple calculation is often part of bigger geometric proofs.
2. Architecture and Engineering:
   When designing structures like bridges or roof trusses, engineers use the concept of alternate interior angles to ensure stability. Correct angles guarantee that forces are evenly distributed, preventing collapse or structural damage.
3. Navigation and Mapping:
   In cartography, alternate interior angles help in measuring slopes and angles between roads or railway tracks. Surveyors rely on this principle to ensure roads and tracks are parallel or maintain correct angles for safety.

Common Mistakes and Misunderstandings

Despite its simplicity, students often make mistakes when dealing with alternate interior angles. Some common errors include:

• Confusing Alternate Interior Angles with Exterior Angles: Exterior angles lie outside the parallel lines. Confusing the two can lead to incorrect answers.
• Assuming Lines Are Parallel Without Verification: Remember, the equality of alternate interior angles proves that lines are parallel, not the other way around. Assuming lines are parallel without checking the angles can lead to faulty reasoning.
• Ignoring the Transversal: Some learners identify angles inside two lines but forget that the transversal must cut across the lines. Without the transversal, alternate interior angles do not exist.

Being aware of these mistakes helps in avoiding errors and strengthens understanding of the concept.

Alternate Interior Angles and Other Angle Relationships

Alternate interior angles are closely related to other angle types in geometry, which makes them even more versatile:

• Corresponding Angles: These angles are in the same position on different intersections of the transversal. If lines are parallel, corresponding angles are equal.
• Alternate Exterior Angles: Like alternate interior angles, but they lie outside the parallel lines.
• Vertically Opposite Angles: Formed when two lines intersect, these angles are equal but are not necessarily related to parallel lines.

Understanding these relationships makes solving complex geometry problems easier and faster.

Why Mastering Alternate Interior Angles Is Beneficial

Mastering alternate interior angles is not just about passing exams. It builds critical thinking, problem-solving skills, and a deeper appreciation for mathematics. Here are some key benefits:

1. Enhanced Logical Thinking: Learning the properties of alternate interior angles encourages logical reasoning. Students develop the ability to analyze shapes, lines, and angles systematically.
2. Better Performance in Exams: Geometry questions often involve angle relationships. A solid understanding of alternate interior angles saves time and ensures accuracy.
3. Preparation for Advanced Mathematics: High-level math topics like trigonometry, coordinate geometry, and calculus often rely on fundamental concepts like alternate interior angles. Early mastery creates a strong foundation for future studies.
4. Practical Everyday Skills: From designing furniture to understanding maps, alternate interior angles appear in many real-life scenarios. Recognizing them improves spatial awareness and practical problem-solving.

Conclusion

Alternate interior angles, though a basic concept in geometry, hold immense power in both theoretical and practical applications. They simplify complex problems, support critical reasoning, and appear in real-world scenarios ranging from engineering to art. Understanding them fosters confidence in mathematics and builds a strong foundation for more advanced topics.

Whether you are a student struggling with geometry or a professional using angles in your daily work, appreciating the beauty and utility of alternate interior angles can turn what seems like a simple rule into a powerful tool. By practicing, visualizing, and applying this concept, anyone can master it and enjoy the satisfaction of solving geometric puzzles with ease.

In the end, alternate interior angles remind us that even in mathematics, small details hold extraordinary importance. Their simple equality property opens doors to a world of geometric reasoning, proving that understanding angles is not just useful—it is genuinely rewarding.